سی ثانیه پای صحبت برایان دایسون

فرض کنید زندگی همچون یک بازی است.قاعده این بازی چنین است که بایستی پنج توپ را در آن واحد در هوا نگهدارید و مانع افتادنشان برزمین شوید. جنس یکی از آن توپها ازلاستیک بوده و باقی آنها  شیشه ای هستند. پر واضح است که در صورت افتادن توپ پلاستیکی بر روی زمین، دوباره نوسان کرده و بالا خواهد آمد، اما آن چهار توپ دیگر به محض برخورد ، کاملا شکسته و خرد میشوند. او در ادامه میگوید : آن چهار توپ شیشه ای عبارتند از خانواده، سلامتی،  دوستان و روح  خودتان  و توپ لاستیکی همان کارتان است. کار را برهیچ یک از عوامل فوق ترجیح ندهید، چون همیشه کاری برای کاسبی وجود دارد ولی دوستی که از دست رفت دیگر بر نمیگردد، خانواده ای که از هم
 پاشید دیگر جمع نمیشود،‌ سلامتی از دست رفته باز نمیگردد و روح آزرده دیگر آرامشی ندارد. 

*

خواندنی و بعد اندکی به فکر رفتن

عکسی است که فضاپیمای وویجر از زمین گرفته است. عکسی که زمین را در فضای بیکران نشان می دهد.  کارل ساگان کیهان شناس آمریکایی کتابی با همین عنوان نوشته است. در قسمتی از این کتاب می خوانیم:

کتاب حساب دیفرانسیل و انتگرال جدیدالتألیف

در کتاب جدیدالتألیف حساب دیفرانسیل و انتگرال، ساختار موضوعی، بیش از 80 درصد مانند ساختار موضوعی کتاب قبلی است اما روش آموزشی این کتاب با کتاب قبلی کاملاً متفاوت و بیشتر شبیه و هماهنگ با کتاب‌های جدیدالتألیف می‌باشد.

ساختار کتاب عبارت است:

فصل اول - مجموعه اعداد

فصل دوم - دنباله‌ها و سری‌ها

فصل سوم - حد و پیوستگی

فصل چهارم - مشتق و کاربردها

فصل پنجم - انتگرال

قضیه استوارت

قضیه استوارت، (به انگلیسی: Stewart's theorem) در هندسه اندازه پاره‌خط وارد از یک رأس بر ضلع روبرو را بر حسب اندازه اضلاع مثلث و دو پاره‌خط ایجاد شده بر روی ضلع می‌دهد. به افتخار ریاضیدان اسکاتلندی متیو استوارت که در مقاله‌ای در سال ۱۷۴۸ این قضیه را منتشر کرد، این قضیه را قضیه استوارت نامیده‌اند.
اگر b ،a و c طول اضلاع مثلت و p طول پاره خط مورد نظر باشد، آنگاه:

a(p²+xy)=b²x+c²y

که x و y طول دو پاره‌خط ایجاد شده بر ضلع هستند. 

اثبات را در ادامه ببینید.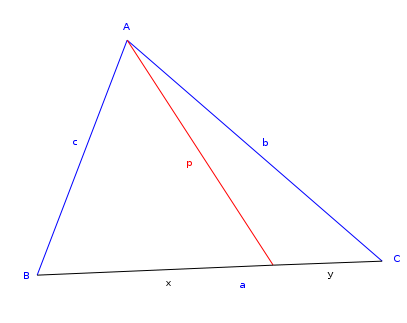

مدرسه عشق (شعری از مرحوم مجتبی کاشانی)

 در مجالی که برایم باقیست
باز همراه شما مدرسه ای می سازیم
که در آن همواره اول صبح
به زبانی ساده
مهر تدریس کنند
و بگویند خدا
خالق زیبایی
و سراینده ی عشق
آفریننده ماست